

Une carte géographique avec des lignes de niveaux f(x, y)=c0
Une carte météo, avec les lignes isobares
Une surface implicite est définie par une fonction f de R3 dans R et une constante c. On peut illustrer par deux exemples de fonctions de R2 dans R
|
|
|
|
Une carte géographique avec des lignes de niveaux f(x, y)=c0 |
Une carte météo, avec les lignes isobares |
Dans notre cas, on peut imaginer que les primitives sont des sources de chaleur : plus on s´éloigne de la source, plus la chaleur décroît. Ainsi, à tout point de l'espace est associé une valeur de potentiel qui est la somme des contributions de chaque source. On définit alors une surface S comme étant l'ensemble des points ayant une certaine valeur T.
Les figures suivantes illustrent cette définition : à gauche sont représentées les iso-courbes correspondant à des valeurs T de plus en plus petites. A droite est tracée la surface correspondant à une valeur T particulière. Ces deux figures sont des coupes.
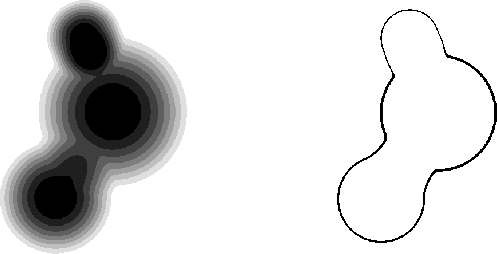
Il n'est cependant pas possible de représenter des valeurs continues dans la mémoire d'un ordinateur. Il va falloir discrétiser le problème. On va par conséquent découper notre espace en cubes élémentaires. On affectera à chacun des sommets du cube le potentiel lui correspondant. On obtient donc une grille 3D de valeurs, qui va nous servir à définir notre surface. Il nous faut alors choisir la valeur du potentiel caractérisant notre surface.
Prenons une grille 2D pour visualiser:
|
|
|
|
grille de valeurs utilisée |
la courbe de niveau doit passer par le potentiel 0.5 |
A partir de cet exemple, il est facile d'étendre aux iso surface dans une scène 3D. Au lieu d'obtenir une ligne, qui suit la valeur définie, il s'agira d'une surface.