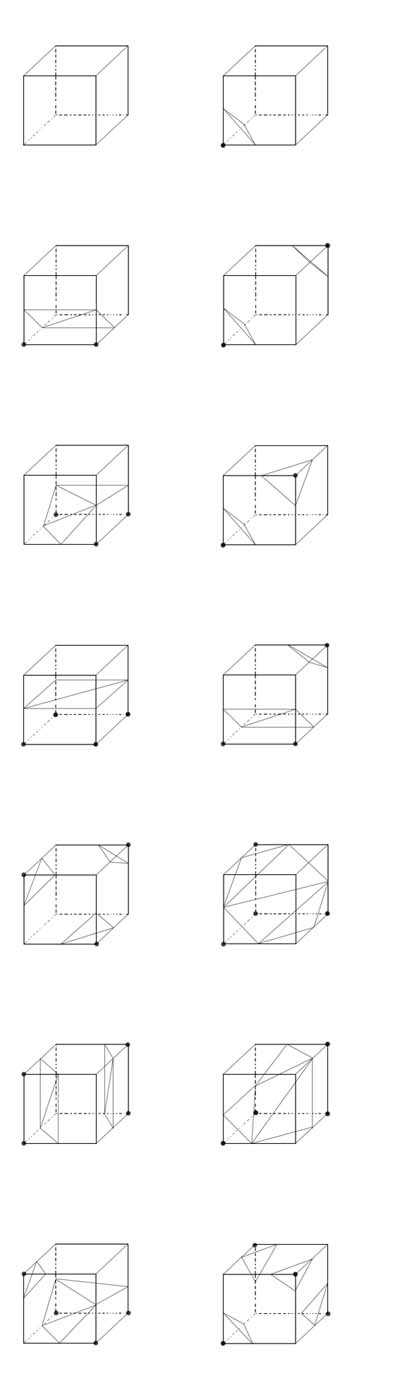
Pour facettiser ,et donc visualiser, les surfaces implicites, nous utilisons la technique des "marching cubes". Pour chaque cube unité de cette grille, il s'agit de savoir si la surface passe par celui-ci et de quelle manière. Pour ce faire, nous cherchons les sommets dont les potentiels sont supérieurs (respectivement inférieur) à la valeur d'iso-potentiel, et nous les marquons par 0 (respectivement 1). Nous obtenons ainsi 256 configurations. Par rotations, symétries et dualité, nous sommes ramenés à 14 cas génériques.

les quatorze cas génériques
Pour chaque point d'ancrage de la facette, on peut choisir la rapidité en prenant la moitié du segment ou plus réaliste, on le place en fonction des potentiels des extrémités : si le point x1 est au potentiel p1 et le point x2 au potentiel p2, on ancre en t.x1+(1-t).x2, où t=abs(p2-0.5)/(abs(p1-0.5)+abs(p2-0.5)).
Pour coder les cubes, ayant 8 sommets étant soit à 1, soit à 0, on se sert des octets en mettant le premier sommet en dernière position.
On peut raffiner le système en découpant le cube en six tétraèdres.
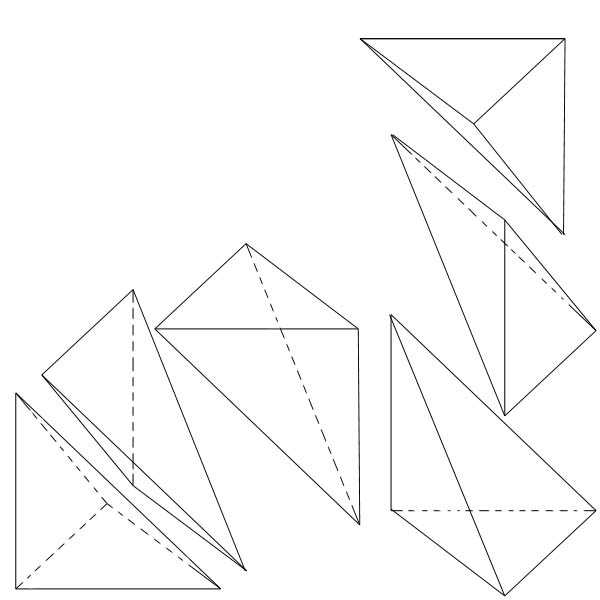
On se ramène alors à 3 cas génériques. Les deux ci-dessous auxquels il faut ajouter les cas vide.
Chaque tétraèdre est lui aussi codé sur un octet mais avec les quatre premiers bits à 0. Pour savoir comment passe la surface, on compare l'octet aux sept octets de références. Reste le problème de passer d'une configuration de cube, avec des octets classiques, à celle de tétraèdre, avec des octets commençant par quatre 0.
Prenons un exemple : comment coder le tétraèdre passant par les sommets 1,2,4 et 5? Tout d'abord dans quel ordre le parcourir et est-ce important? La réponse est "oui" pour que les facettes tracées le soient toutes dans le même sens afin de pouvoir y associer des normales. Sur les quatre points, on fixe le sommet puis on parcours les autres avec la règle du tire-bouchon. On a donc le tétraèdre (4,5,2,1). On considère le code du cube :
| bit | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| valeur du bit, soit 1, soit 0 | x8 | x7 | x6 | x5 | x4 | x3 | x2 | x1 |
| exemple | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
et on veut obtenir le code du tétraèdre :
| bit | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| valeur du bit, soit 1, soit 0 | 0 | 0 | 0 | 0 | x4 | x2 | x5 | x1 |
| exemple | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
On utilise les masques suivants :
| e1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| e2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| e3 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| e4 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| e5 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| e6 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| e7 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| e8 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
et on effectue les opérations logiques suivantes :
| c&e1 |
|
||||||||
| (c&e1)<<3 |
|
||||||||
| c&e5 |
|
||||||||
| (c&e5)>>3 |
|
||||||||
| c&e2 |
|
||||||||
| (c&e2)<<1 |
|
||||||||
| c&e4 |
|
||||||||
| (c&e4)>>3 |
|
||||||||
| ((c&e1)<<3)l((c&e5)>>3) |
|
||||||||
| (c&e1)l((c&e5)>>3)l((c&e2)<<1) |
|
||||||||
| (c&e1)l((c&e5)>>3)l((c&e2)<<1)l(c&e4) |
|
On code ainsi les tétraèdres (4,5,2,1), (2, 4, 5, 8), (2, 3, 4, 8), (2, 5, 6, 8), (2, 6, 3, 8), (3, 8, 6, 7) puis on les compare aux huit tétraèdres de référence (que l'on a obtenu à partir des 16 cas initiaux auxquels on a ôter les cas duaux : de 0000.0100 et 0000.1011 on peut éliminer le second) afin de tracer les facettes.